國內石材空心圓柱異型弧板加工已經很普遍了。在實際加工過程中,開料(留余量)、粗磨、精打磨等都用得著弦長,做到心中有數。
我們的技術加工人員,有時并不是不會計算,而是計算起來比較麻煩、費時,不小心還會弄錯。有沒有簡單的方法呢?像查詢“代數表”一樣查“均分弦長值”?
空心圓柱的加工方法:
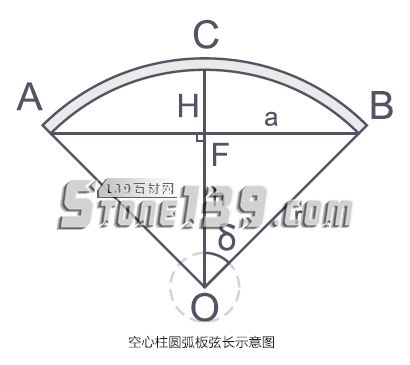
如圖,⊙O中均分弦長為AB,OC為∠AOB 的角平分錢,OC⊥AB 交點為F,圓周均分值n(塊),∠BOC =1/2圓心角=360/2n。
為方便表達,設∠BOC=∠δ,設半弦長FB為a,弦的圓心距OF為h、半徑為r,即在 Rt△OFB中:
半弦長a=sinδ·r,則:弦長=sinδ·直徑。
如果我們要個方便簡單的計算方法,即只要知道均分值,即可查出等分系數,設此圓“等分系數”為“K”,
即K=sinδ=sinδ(360/2n)
已知圓的圓周土均勻分值n,查詢等分系數K值即可快速算出弦長:
弦長=K·直徑(*公式①)
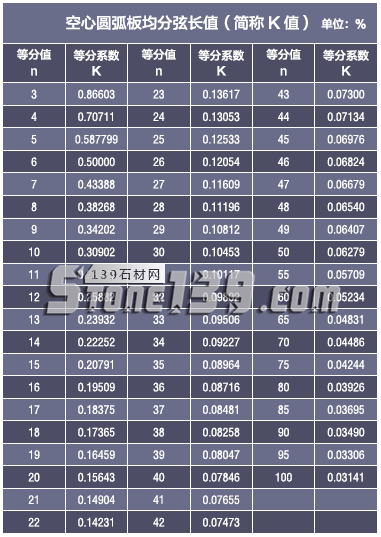
下面“圓均分弦長系數”K值表或許能夠給你帶來方便(如下圖):
例:直徑為2000mm的空心圓柱,均分值n=8,求對應均分件弦長。
解:查詢下表得n=8 時對應的K值為0.38268,代入公式①
8分弦長=K(注:n=8)·直徑
=0.38268·2000mm=765.36mm
實際運用中,有時還要計算圓弧板的“拱高”。
設拱高為FC=H,則:H=r-h
又,在RT△OFB中,h=cos∠δ·r
拱高H= r·(l-cos∠δ)
 客服熱線:
客服熱線:















